Cách tính diện tích tam giác: Thường, Vuông, Cân, Đều và ví dụ minh họa
Bạn đang phân vân không nhớ rõ cách tính diện tích các loại tam giác thường, vuông, cân, đều. Bài viết này, ThuThuatTinHoc.vn sẽ hướng dẫn bạn tổng hợp các cách tính diện tích của các loại tam giác.
1. Cách tính diện tích tam giác thường
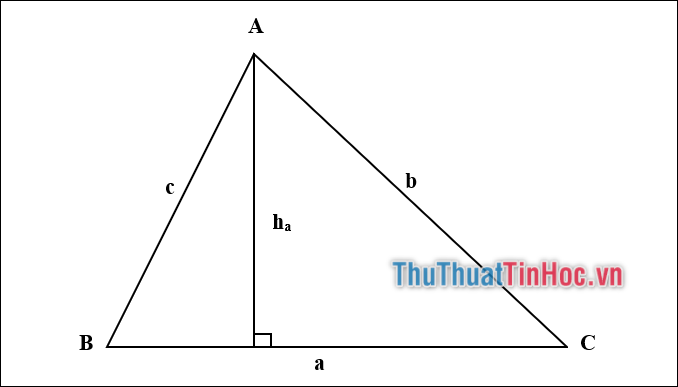
Công thức được sử dụng nhiều nhất đó là: \({S_{ABC}} = \frac{1}{2}a.{h_a} = \frac{1}{2}b.{h_b} = \frac{1}{2}c.{h_c}\)
Hay diễn giải ra là: Diện tích tam giác được tính bằng một nửa (1 phần 2) tích của chiều cao hạ từ đỉnh với chiều dài cạnh đối diện đỉnh đó.
Ví dụ:
Cho chiều dài \({h_a}\) = 3 (cm) ; cạnh a = BC = 6 (cm) \( \Rightarrow \) \({S_{ABC}} = \frac{1}{2}6.3 = 9\).
Ngoài ra còn một số công thức cũng có thể tính được diện tích tam giác thường như:
- Trường hợp biết độ dài 2 cạnh và sin góc hợp bởi 2 cạnh đó:
\({S_{ABC}} = \frac{1}{2}a.b.{\mathop{\rm Sin}\nolimits} \widehat C = \frac{1}{2}a.c.{\mathop{\rm Sin}\nolimits} \widehat B = \frac{1}{2}b.c.{\mathop{\rm Sin}\nolimits} \widehat A\)
- Trường hợp biết nửa chu vi tam giác (p) và độ dài của 3 cạnh a, b, c:
\({S_{ABC}} = \sqrt {p(p - a)(p - b)(p - c)} \)
- Trường hợp biết nửa chu vi tam giác (p) và bán kính đường tròn nội tiếp tam giác (r).
\({S_{ABC}} = p.r\)
- Trường hợp biết bán kính đường tròn ngoại tiếp tam giác (R) và độ dài 3 cạnh của tam giác.
\({S_{ABC}} = \frac{{abc}}{{4R}}\)
2. Cách tính diện tích tam giác vuông
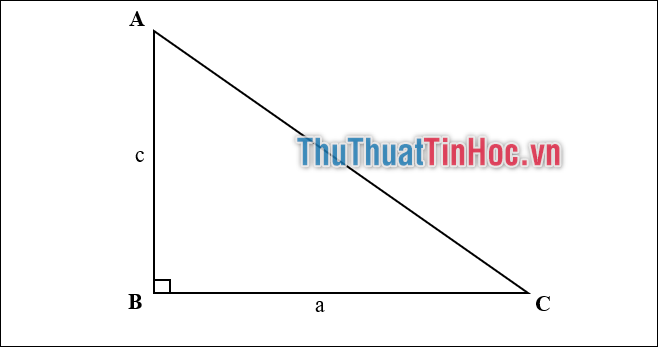
Công thức: \({S_{ABC}} = \frac{1}{2}a.c\)
Diễn giải: Diện tích của tam giác vuông được tính bằng một nửa (1 phần 2) tích của hai cạnh góc vuông.
Ví dụ:
Cho tam giác ABC vuông tại B có cạnh AB = 3cm ; BC = 4cm.
\( \Rightarrow {S_{ABC}} = \frac{1}{2}3.4 = 6(cm)\)
3. Cách tính diện tích tam giác cân
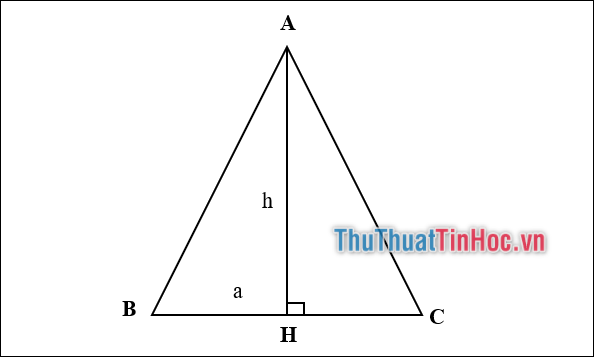
Công thức: \({S_{ABC}} = \frac{1}{2}a.h\)
Diễn giải: Diện tích của tam giác cân bằng một nửa (1 phần 2) tích của chiều dài cạnh đáy với chiều dài đường cao hạ từ đỉnh.
Ví dụ:
Cho tam giác ABC cân tại A, có chiều cao AH = 6cm; cạnh BC = 5cm.
\( \Rightarrow {S_{ABC}} = \frac{1}{2}6.5 = 15(cm)\)
4. Cách tính diện tích tam giác đều
Công thức: \({S_{ABC}} = {a^2}.\frac{{\sqrt 3 }}{4}\)
Với a là độ dài của cạnh tam giác.
Ví dụ: Cho tam giác đều ABC có cạnh a = 4cm \( \Rightarrow {S_{ABC}} = {4^2}.\frac{{\sqrt 3 }}{4} = 4\sqrt 3 (cm)\)
Cảm ơn các bạn đã theo dõi bài viết!!!

















Viết bình luận